模拟退火算法(Simulated Annealing)——简析

什么是模拟退火算法？

模拟退火算法，（英语：Simulated annealing，缩写作SA）是一种通用概率算法，常用来在一定时间内寻找在一个很大搜寻空间中的近似最优解。通过模拟物理上退火方法，经过N次迭代（退火），逼近函数的上的一个最值（最大或者最小值）。比如逼近这个函数的最大值A点：模拟退火算法与初始值无关，算法求得的解与初始解状态S（是算法迭代的起点）无关；模拟退火算法具有渐近收敛性，已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法；模拟退火算法具有并行性。（看不懂无所谓）

模拟退火是怎么来的？

模拟退火算法的思想借鉴于固体的退火原理，退火是将材料加热后再经特定速率冷却，目的是增大晶粒的体积，并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置，加热使能量变大，原子会离开原来位置，而随机在其他位置中移动。退火冷却时速度较慢，使得原子有较多可能可以找到内能比原先更低的位置。模拟退火的原理也和金属退火的原理近似：我们将热力学的理论套用到统计学上，将搜寻空间内每一点想像成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。

总结如下：

温度高->运动速度快（温度低->运动速度慢）
温度是缓慢（想象成特别慢的那种）降低的
温度基本不再变化后，趋于有序(最后内能达到最小，也就是接近最优)

我们通过模拟这个操作，使得我们需要的答案“趋于有序”，也就是最靠近需要的值（最值）。可以证明，模拟退火算法所得解依概率收敛到全局最优解。

演算步骤

什么？你看不懂上面的？直接跳过，看下面的步骤即可。如果我们要求函数的极大值

设置初始温度$T_0$和降温速度$\Delta T$（$\Delta T$越接近1降温速度越慢），令当前温度$T_{current} = T_0$,并设置一个终止温度$T_{end}$和一个随机的初始解$x_0$,令当前解$x_i = x_0$。
使当前温度发生变化（降温），$T_{current} = \Delta T \times T_{current}$，$\Delta T$的值取0.5~1之间。
计算当前状态$x_0$下的函数值, 根据当前温度进行随机扰动，产生一个新的解$x_i$，比较新解是否比旧解大（如果求函数最大值）$f(x_i)−f(x_0)$。
若$f(x_i)−f(x_0) > 0$，则接受该解，否则以概率$P = e^{\frac{\Delta f}{kT}}$接受该解。
比较$T_{current}$与$T_{end}$的大小，若$T_{current} < T_{end}$，则终止，否则循环执行234。

可以看出，算法实际上是两层循环嵌套，外层循环控制温度，内层循环来进行扰动产生新解。

具体做法

第一步

首先，模拟退火是一种迭代算法，这意味着它需要循环。因此，我们需要先设定一个初始的温度$T$（比如说1000）和降温系数$\Delta T$ 。

第二步

我们要求解的答案无非是两个：自变量$x$和对应函数的最大值$f(x)$。而模拟退火算法的核心步骤，分为新解的产生和接受新解两部分：（接受新解采用的是Metropolis准则：若Δt′<0则接受S′作为新的当前解S，否则以概率exp（-Δt′/T）接受S′作为新的当前解S。有兴趣可以了解一下，没兴趣就不用理，这里不过多解释。）

我们在函数定义域内随机找一点$x_0$，以这个点作为我们的初始值（相当于物体里的一个粒子），由函数算得$f(x_0)$ 。
刚才我们说了$x_0$相当于是一个粒子，所以我们会进行一个无序运动，也就是向左或者向右随机移动到$x_1$。 是的，是随机移动，可能向左，也可能向右，但是请记住一个关键点：移动的幅度和当前的温度$T$有关。温度$T$越大，移动的幅度越大。温度$T$越小，移动的幅度就越小。这是在模拟粒子无序运动的状态。
接受更"好"的状态假设我们移动到了$x_1$处，且这个点对应的$f(x_1)$很明显答案是优于（大于）当前的$f(x_0)$的。因此我们将答案进行更新。也就是将初始值进行替换：将$x_1$设为初始点。这是一种贪心的思想。
以一定概率接受更差的状态为什么我们要接受一个更加差的状态呢？因为可能在一个较差的状态旁边会出现一个更加高的山峰（更优解）如果我们鼠目寸光，只盯着右半区，很容易随着温度的下降、左右跳转幅度的减小而迷失自己，最后困死在小山丘中。而我们如果找到了左边山峰的低点，以一定的概率接受了它（概率大小和温度以及当前的值的关键程度有关），会在跳转幅度减少之前，尽可能找到最优点。

那么我们以多少的概率去接受它呢？根据Metropolis准则，这个概率为 $$ e^{\frac{\Delta f}{kT}} $$ 这里解释一下各个变量： $e^x$ ：以$e$（自然常数）为底的指数函数高中就学了，不解释。这里$e^x$的值一定不能大于1（概率不能大于1）。 $k$：玻尔兹曼常数，我们在代码中不会用到，直接认为$k=1$，即概率表达式变成了$e^{\frac{\Delta f}{T}}$。 $T$：当前温度。 $\Delta f$：重点！！！ 由高中知识，若要使$e^x$这个函数的值不大于1，则x（e的指数）一定不能大于0。我们想要函数$e^x$来代表一个概率值，一定要让$e^x$的值域属于(0,1)，所以$\frac{\Delta f}{kT}$必须是个负数。但是$kT$在我们的模拟中一定是正数，那么$\Delta f$必须是个负数！其实$\Delta f$就是当前解的函数值与目标解函数值之差，$\Delta f=−|f(x_0)−f(x_1)|$，并且一定是个负数。这个需要具体问题具体分析。

比如现在我们求一个函数的最大值，那么如果$f(x_0)<f(x_1)$了，那就说明结果变好了，我们肯定选择它（见第4点）

如果$f(x_0)>f(x_1)$，那就说明结果变差了，我们需要概率选择它，因此 $$\Delta f=−(f(x_0)−f(x_1))$$

所以总结一下就是：

随机后的函数值如果结果更好，我们一定选择它。
随机后的函数值如果结果更差，我们以$e^{\frac{\Delta f}{kT}}$的概率接受它。

程序框图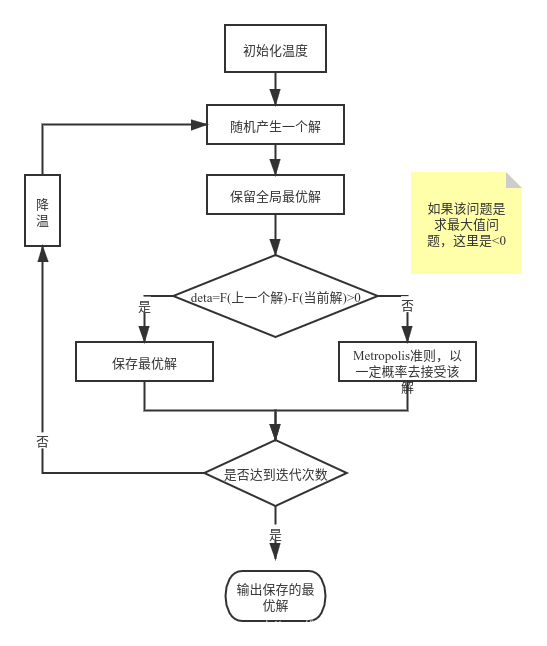： 关于接受概率$e^x$和Δf以及kT的关系：

当kT越大时(温度越高)，由于$\Delta f$是一个负数，所以算出来的值会越大。比如-1 / 1000 等于 -0.001，很明显-0.001 > -1，由于$e^x$是个单调递增函数，所以温度越高时，接受的概率就越大。 $\Delta f$越小，说明答案越糟糕，那么接受的概率就越小。

伪代码

注：对代码中的函数作出解释：

rand()函数 rand()函数可以默认拿到[0,32767]内的随机整数 RAND_MAX = 32767，可以看作常量。本质是宏定义: #define RAND_MAX 32767 rand() * 2 的范围是[0,32767 * 2] rand() * 2 - RAND_MAX 的范围是[-32767, 32767]
exp()函数：exp(x)代表$e^x$
exp((df - f) / T) * RAND_MAX > rand() 目的是要概率接受，但是$e^x$是个准确值，所以从理论上我们可以生成一个(0,1)的随机数，如果$e^x$比(0,1)这个随机数要大，那么我们就接受。但是由于rand()只能产生[0,32767]内的随机整数，化成小数太过麻烦。所以我们可以把左边乘以RAND_MAX（也就是把概率同时扩大32767倍），效果就等同于$e^x$比(0,1)了。

double T = 2000; //代表开始的温度
double dT = 0.99; //代表系数delta T
double eps = 1e-14; //相当于0.0000000000000001

//用自变量计算函数值,这里可能存在多个自变量对应一个函数值的情况，比如f(x,y)
double func(int x, ... ) {
    //这里是对函数值进行计算
    double ans = .......
    return ans;
}
//原始值
double x = rand(); //x0取随机值
double f = func(x,...); //通过自变量算出f(x0)的值
while(T > eps) {
    //--------------
    //这里是每一次退火的操作
    
    //x1可以左右随机移动，幅度和温度T正相关，所以*T
    //注意这里移动可以左右移动，但是也可以单向移动
    //关于rand()详细见开头注的①
    double dx = x + (2*rand() - RAND_MAX) * T; 
    
    //让x落在定义域内，如果没在里面，就重新随机。题目有要求需要写，否则不用写
    // ================
    while(x > ? || x < ? ...) {
        double dx = x + (2*rand() - RAND_MAX) * T; 
    }
    // ================
    
    //求出f(x1)的值
    double df = func(dx);
    //这里需要具体问题具体分析，我们要接受更加优秀的情况。可能是df < f(比如求最小值）
    if(f < df) {
        f = df; x = dx;  [...,y = dy;] // 接受，替换值，如果多个自变量，那么都替换
    }
    //否则概率接受，注意这里df-f也要具体问题具体分析。
    //详细见开头注的②③
    else if(exp((df - f) / T) * RAND_MAX > rand()) {
        f = df; x = dx;  [...y = dy;] // 接受，替换值，如果多个自变量，那么都替换
    }
	//--------------
    T = T * dT; //温度每次下降一点点， T * 0.99
}
//最后输出靠近最优的自变量x值，和函数值f(x)
cout << x << " " << f << endl;

什么是模拟退火算法？#

模拟退火是怎么来的？#

演算步骤#

具体做法#

第一步#

第二步#

伪代码#

什么是模拟退火算法？

模拟退火是怎么来的？

演算步骤

具体做法

第一步

第二步

伪代码